Trajectories in Unity
Firstly I want to start off by saying this post will include a lot of maths and code and assumes some background knowledge of Unity, as well as Newtonian and vector mathematics.
My goal was to get the trajectory for a grenade to use in my game, Quantum Robot. I wanted this trajectory to start from the weapon and land at a point in front of the player’s head/camera. The problem with this is that the weapon is offset in all 3 dimensions so things get complicated fast. Another thing I wanted was to get the trajectory path to the player line up with the projectile once it was launched.
To display the trajectory we can used a simple LineRenderer, and to make the projectile move we can apply motion to a Rigidbody.
I decided that the start of the trajectory path was more important so we can make the thickness of the LineRenderer decrease over it's path. By doing this we do not have to worry about if the projectile is going to land below the height it started at as the line would be near unseeable by that point anyway. To change the thickness we can use the Width curve in the inspector.
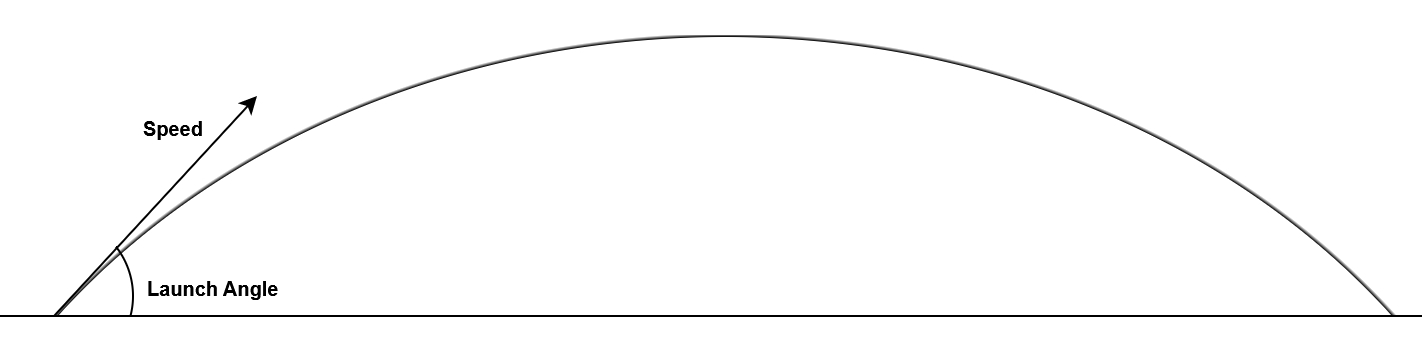
To get the trajectory started we can simply think of it in 2 dimensions, height and distance. Starting with values for speed and angle of launch we can use the trajectory formulas.
The projectile follows this equation of motion:
y = x*tan(launch angle) - (x^2 * gravity) / (2 * speed^2 + cos^2(launch angle))
With this equation we can render the path. To do this we need to pick either x or y and vary them to order to calculate the other one and plot the values at each point. As you should be able to tell from the equation, we are going to vary x and calculate y.
We are going to take values for x at equal distances from 0 to the distance the projectile hits the ground.
for (int i = 0; i < numberOfLines + 1; i++)
{
// cast numberOfLines to float so the answer is calculated as a float
float t = i / (float)numberOfLines;
float x = x * trajectoryDistance;
// calculate y
}
Initially I thought we could use the simple distance equation as we do not care about if the projectile lands below the start of the start height.
Distance = (speed^2 * sin(2 * launch angle)) / gravity
However this formula does not work if you have negative angles, so whenever the player looks down the trajectory would flip and face behind the player. To fix this we need to use a formula that takes initial height into account. Derivation can be found here.
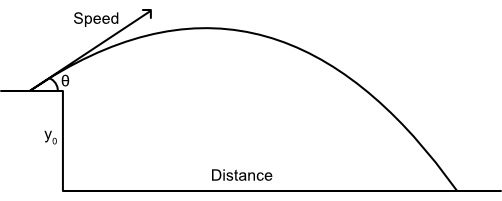
Converting that formula to C# we get this
float TrajectoryDistance(float speed, float angle, float gravity, float initialHeight = 0f)
{
float xSpeed = Mathf.Cos(angle) * speed;
float ySpeed = Mathf.Sin(angle) * speed;
return (xSpeed / gravity) * (ySpeed + Mathf.Sqrt(ySpeed * ySpeed + 2f * gravity * initialHeight));
}
Now we have all of the parts to get our trajectory to work in 2 dimensions. The LineRenerer draws linear lines between a set of points. We want to calculate x and y at points along the trajectory curve, we should calculate atleast 10 points so that our line looks like a curve.
void RenderArc(float speed, float angle, int numberOfLines)
{
// 1 point for the start of each line + 1 at the end of the arc.
this.lineRenderer.positionCount = numberOfLines + 1;
Vector3[] positions = new Vector3[numberOfLines + 1];
// the angle must be in radian in order to use Unity's Mathf
float radianAngle = Mathf.Deg2Rad * angle;
// we want the negative value as our formula's assume gravity is negative.
float gravity = (- Physics.gravity.y);
float trajectoryDistance = TrajectoryDistance(speed, radianAngle, gravity);
for (int i = 0; i < numberOfLines +1; i++)
{
// cast numberOfLines to float so the answer is calculated as a float
float t = i / (float)numberOfLines;
float x = x * trajectoryDistance;
float y = x * Mathf.Tan(radianAngle) - ((gravity * x * x) / (2 * speed * speed * Mathf.Cos(radianAngle) * Mathf.Cos(radianAngle)));
position[i] = (y * Vector3.up) + (x * player.transform.forward) + player.transform.position;
}
lineRenderer.SetPositions(positions);
}
A few notes about the position as we convert x and y to a vector. y should be the global up. x should be the local forward, this is so that the trajectory is always facing the same direction as our GameObject. Lastly we need to make sure that the trajectory moves with the GameObject.
We should now have a working trajectory starting at the GameObject that has the script attached. In order to make this work with an offset only requires minor changes.
First we should set up our objects in Unity so that this will be easy to do. The LineRenderer and script are put on a child of the weapon and the weapon is a child of the player’s head. In my setup the player’s head controls rotation up and down, while the player(root) object controls rotation left and right.
The target location for the grenade will be the forward direction from the player object, but the starting location of the grenade will be the weapon.
The height offset is easy to sort out, we can just add the local y position of the weapon to TrajectoryDistance function call.
TrajectoryDistance(speed, radianAngle, gravity, transform.position.y);
In order to calculate the direction you will need the player’s transform, the weapon’s transform and the trajectory distance. We will add vectors as show in the diagram. We do not want the result vector to have any y component as we have already dealt with that offset. Lastly we normalize the vector as we only want it’s direction.
Vector3 CalculateTrajectoryDirection()
{
Vector3 direction =
player.transform.forward * this.TrajectoryDistance
+ player.transform.position
- weapon.transform.position;
// we only want the vector in the xz direction
direction.y = 0;
// only want direction not magnitude
return direction.normalized;
}
We can now use that direction to replace transform.forward:
position[i] = (y * Vector3.up) + (x * direction) + transform.position;
The angle the grenade is launched at can be calculated in a few ways, the easiest way with this setup is to use the player’s head rotation. We also need to clamp the angle between -90 and 90 degrees so the player can only throw forward. I have also given the trajectory an initial angle of 30 degrees.
float CalculateAngle() {
float headAngle = -1 * playerHead.transform.rotation.eulerAngles.x;
float angle = ClampAngle(headAngle + 30, -90, 89.99);
return angle;
}
float ClampAngle(float angle, float min, float max)
{
// makes sure angle is between -180 and 180
while (angle <= -180)
{
angle += 360;
}
while (angle > 180)
{
angle -= 360;
}
// clamps angle within min and max
return Mathf.Clamp(angle, min, max);
}
The angle may need to be negative depending of the setup, in my case it is.
Moving on to the projectile itself. To make this work with the values we have already calculated we can use rigidbody.velocity when we launch the grenade and then leave Unity to deal with the rest. To calculate the velocity we can use the following
Vector3 calculateVelocity(float speed, Vector3 direction, float radianAngle)
{
float yDirection = Mathf.Tan(radianAngle);
Vector3 finalDirection = new Vector3(direction.x, yDirection, direction.z);
return speed * finalDirection.normalized;
}
For the y direction we need to calculate the ratio of y motion to the combined x and z motion. Since we normalized direction earlier the combined x and z is 1 so we can use Tan to calculate y. We can then normalize the vector to get the new direction and multiple by speed.
We should now be finished and have a rendered trajectory and a projectile that follows it.
